Sample 8 FIT


DLG(E='#Explain', B='OK')
#Explain FIT determines the parameters of a a mathematical shape to agree with some measured data points using the Levenberg-Marquard method. .1 Plot the data .2 Think of a mathematical function that might describe the data. .3 Input/output parameters of FIT: . array p . column 1: actual parameters (input) . column 2: standard deviation (output) . column 3 etc parameter correlations (output) . array XMC . column 1: the independent variable x (input) . column 2: the observed values M (input) . column 3 calculated values C (output) . string Residual (optional output) . Residual=... lists ((SUM(C - M)^2))^(1/2) / rows(XMC) and iters . FIT returns the number of iterations performed. . FIT is called by either .4a iters = FIT(Theory="mytheory(parameters, Xval_Ymeas_Ycalc)") . The function mytheory has to calculate the 3rd column of . Xval_Ymeas_Ycal as a function of parameters and Xval . (see Functionns DampedOscillation and Ellipse) . or if Theory can be written as a 1-liner: .4b iters = FIT(Theory="XMC($,3)=func(XMC,p,$)", Parms=p, XMY=XMC) . (examples see this sample script) .5 FIT succeeded if iterations > 0 and . no NaN (not a number) appear in the correlations table.
SET(arr=shapes(), $name=" ", $theory=" ", parms=" ", xAtoxZ=" ", $startAt=0, $endAt=0, $stepsize=0) LOAD("LeastSquareFit.Settings",shapes) DO test = 1, 1000 $FUNC = 0 DLG(X=0, TI='Select shape and hit OK. If no shape selected: OK will FIT with increased noise.', Array=shapes, XEQ='$FUNC=$numRC', TI="select,Shape ,theory: x=XMC(col1) yobs=XMC(col2) ycalc=XMC(col3),pā‚ pā‚‚ pā‚ƒ etc,from to step", SAVE=0) IF( $FUNC ) !******************************************************** PLOT ******** ARRAY(Name=p, CLeaR=1, Name=XMC, CLeaR=1) $random = 0.001 $name = shapes($FUNC,1) $theory = shapes($FUNC,2) parms = shapes($FUNC,3) xAtoxZ = shapes($FUNC,4) $startAt = DEC(xAtoxZ, 1) $endAt = DEC(xAtoxZ, 2) $stepsize = DEC(xAtoxZ, 3) $stepsize = MAX($stepsize, 0.1) $np = 1 + EDIT(T=parms, Count=' ') SAVE("LeastSquareFit.Settings", shapes) p(1,1) = DEC(parms, 1) ! Start value parm 1 IF($np > 1) p(2,1) = DEC(parms, 2) ! Start value parm 2 IF($np > 2) p(3,1) = DEC(parms, 3) ! Start value parm 3 IF($np > 3) p(4,1) = DEC(parms, 4) ! Start value parm 4 ENDIF ENDIF ENDIF DO i = 1, $np p(i,2) = 0 ! std dev parm i DO j = 3, 3+$np-1 p(i,j) = 0 ! correlation parm i / parm j ENDDO ENDDO j = 0 DO i = $startAt, $endAt, $stepsize j = j + 1 XMC(j,1) = i ! set measured x values in column 1 of array XMC XMC(j,2) = 0 XMC(j,3) = 0 ! make space for CALCULATED y values in column 3 ENDDO ... DLG(X=0,W=1/2, TI='Make "observations"', Array=p, ... Ti=',Original,1. From these parms make "OBSERVED" data (blue circles in graph)', SAVE=0) XEQ($theory) ! set CALCULATED y values XMC($,3) = f(p, XMC($,1)) XMC($,2) = XMC($,3) * RAN(1, $random) ! SIMULATE measured y values based on calculated values XEQ($theory) ! 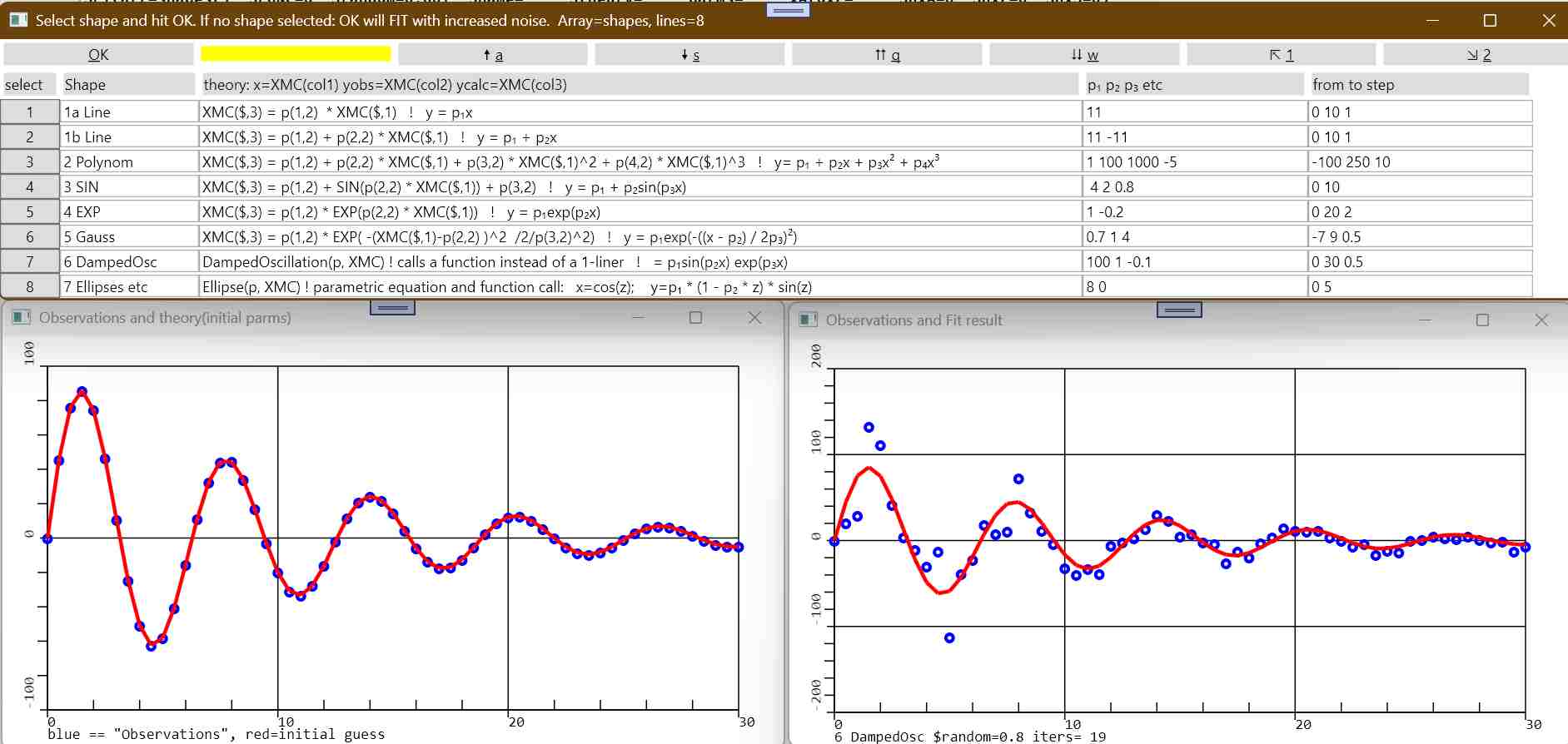set CALCULATED y values XMC($,3) = f(p, XMC($,1)) SET(xMin=1E100, xMax=-1E100, yMin=1E100, yMax=-1E100) xMin = MIN(xMin, XMC($,1)) xMax = MAX(xMax, XMC($,1)) yMin = MIN(yMin, XMC($,2), XMC($,3)) yMax = MAX(yMax, XMC($,2), XMC($,3)) IF(yMin < yMax) DLG(TI='Observations and theory(initial parms)', Rs=2,Cs=2,AX=3, TI='blue == "Observations", red=initial guess', MIN=xMin,MAX=xMax, Y=1,MIN=yMin,MAX=yMax) LINE(AX=3, C=1,XV=XMC, C=2,YV=XMC,S='šŸž‰', D=-9) LINE(AX=3, C=1, XV=XMC, C=3,YV=XMC,W=3, Draw=900) ENDIF ELSE XMC($,2) = XMC($,2) * RAN(1, $random) ! SIMULATE measured noisy y values based on calculated values IF(INDEX($theory, "Damped") > 0) $iters = FIT(Resi=res, Theory="DampedOscillation(p,XMC)") ELSEIF(INDEX($theory, "Ellipse") > 0) $iters = FIT(Resi=res, Theory="Ellipse(p,XMC)") ELSE $iters = FIT(Resi=res, Theory=$theory, Parms=p, XMY=XMC) ENDIF ShowResult(XMC) DLG(X=0, TI='The FIT results. Hit OK to increase noise.' && res, Array=p, Ti=',p result,+- std dev,corr p1,corr p2,corr p3,corr p4', SAVE=0) IF($random < 0.1) $random = 10 * $random ELSE $random = 2 * $random ENDIF ENDIF ENDDO END FUNCTION ShowResult(XMC) SET(xMin=1E100, xMax=-1E100, yMin=1E100, yMax=-1E100) xMin = MIN(xMin, XMC($,1)) xMax = MAX(xMax, XMC($,1)) yMin = MIN(yMin, XMC($,3), XMC($,2)) yMax = MAX(yMax, XMC($,3), XMC($,2)) xTitle = $name && "$random=" & $random && "iters=" && $iters DLG(TI='Observations and Fit result', Rs=2,Cs=2,AX=4, MIN=xMin, MAX=xMax, TIT=xTitle, Y=0, MIN=yMin, MAX=yMax) LINE(AX=4, C=1,XV=XMC, C=2,YV=XMC,S='šŸž‰',W=3, D=-9) LINE(AX=4, Col=1, XV=XMC, Col=3, YV=XMC, W=3, Draw=900) RETURN 0 END FUNCTION DampedOscillation(p, XMC) XMC($,3) = p(1,1) * SIN(p(2,1) * XMC($,1)) * exp(p(3,1) * XMC($,1)) END FUNCTION Ellipse(p, XMC) L = INT(LEN(XMC)) ! length x vector parm(L) = 0 ! make length(parm) == length(x) parm($) = ($ - 1) * $stepsize XMC($,1) = COS( parm($) ) XMC($,3) = p(1,1) * (1 - p(2,1) * $) * SIN( parm($) ) END #Explain FIT determines the parameters of a a mathematical shape to agree with some measured data points using the Levenberg-Marquard method. .1 Plot the data .2 Think of a mathematical function that might describe the data. .3 Input/output parameters of FIT: . array p . column 1: actual parameters (input) . column 2: standard deviation (output) . column 3 etc parameter correlations (output) . array XMC . column 1: the independent variable x (input) . column 2: the observed values M (input) . column 3 calculated values C (output) . string Residual (optional output) . Residual=... lists ((SUM(C - M)^2))^(1/2) / rows(XMC) and iters . FIT returns the number of iterations performed. . FIT is called by either .4a iters = FIT(Theory="mytheory(parameters, Xval_Ymeas_Ycalc)") . The function mytheory has to calculate the 3rd column of . Xval_Ymeas_Ycal as a function of parameters and Xval . (see Functionns DampedOscillation and Ellipse) . or if Theory can be written as a 1-liner: .4b iters = FIT(Theory="XMC($,3)=func(XMC,p,$)", Parms=p, XMY=XMC) . (examples see this sample script) .5 FIT succeeded if iterations > 0 and . no NaN (not a number) appear in the correlations table. ###